GRAFOS
Que es un Grafo
Es un conjunto de puntos,nodos y vértices
Que se puede representar con grafos
Redes de computadoras
Carreteras
Circuitos
Etc..
La mayoría de problema se pueden representa en grafos Recorrer una carretera y volver al sitio origen Encontrar caminos mas cortos en los viajes
Grafo Definicion Normal
G=VE
V el conjunto de vértices y nodos los cuales representan los objetos
E el conjunto de arcos o aristas representan caminos o relaciones
El grado de un nodo se el numero de arcos que inciden
Caso especial (lazo): se considera 2
Grado de un GRAFO: Suma de los grados de los vértices.
Teorema de Grado de un GRAFO: Suma de grados de vértices equivale al doble del número de arcos.
Tipos de Grafos
Grafo Regular
Todos los vértices tienen el mismo grado Si el grado es k, el grafo es k-regular
Grafo Completo
Tiene una arista entre cualquier par de vértices
Mulitgrafo
Es un grafo que tiene arcos múltiples (paralelos) o lazos
Grafo Euleriano
De los grafos no orientados formados por un ciclo euleriano; es decir, aquellos que pueden recorrerse completamente desde un vértice y regresar al punto de origen sin pasar dos veces por la misma arista.

GRAFOS EULERIANOS Cubre todas las líneas de un grafo, comenzando y terminando en un mismo vértice, recorriendo sin repetición y en forma continua todas las líneas de un grafo G cualquiera. Cuando tal recorrido existe, se denomina euleriano y un grafo que se puede trazar mediante un recorrido euleriano se llama grafo euleriano.

De los grafos no orientados formados por un ciclo euleriano; es decir, aquellos que pueden recorrerse completamente desde un vértice y regresar al punto de origen sin pasar dos veces por la misma arista.
GRAFOS EULERIANOS Cubre todas las líneas de un grafo, comenzando y terminando en un mismo vértice, recorriendo sin repetición y en forma continua todas las líneas de un grafo G cualquiera. Cuando tal recorrido existe, se denomina euleriano y un grafo que se puede trazar mediante un recorrido euleriano se llama grafo euleriano.

Grafo Simple
Es un grafo o digrafo que no tiene bucles y que no es un multigrafo
Tipos de Grafos (dirección)
Grafos no dirigidos
Si los pares de nodos de los arcos
no son ordenados
El arco se puede recorrer en ambos sentidos Ej.: u-v
Matriz de adyacencia de un grafo
Todo grafo simple puede ser representado por una matriz, que llamamos matriz de adyacencia.
Se trata de una matriz cuadrada de n filas \times n columnas (siendo n el número de vértices del grafo).
Para construir la matriz de adyacencia, cada elemento a_{ij} vale {{1}} cuando haya una arista que una los vértices i y j. En caso contrario el elemento a_{ij} vale 0.
La matriz de adyacencia, por tanto, estará formada por ceros y unos.
Ejemplo 1
Vamos a construir la matriz de adyacencia del siguiente grafo:
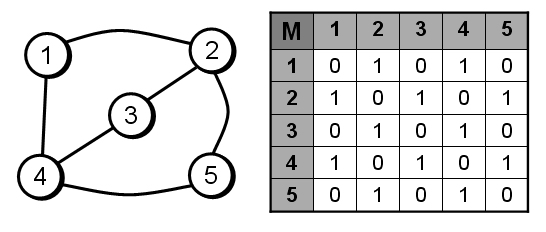
Lista adyacencia de un grafo
En esta estructura de datos la idea es asociar a cada vértice i del grafo una lista que contenga todos aquellos vértices j que sean adyacentes a i y no para todos los posibles arcos que pudieran tener como origen

Matriz de caminos de un grafo
Se utiliza para determinar sin el grafo es fuertemente conectado
S = # caminos de acuerdo al numero de nodos
Si la matriz de camino resultante nos arroja todo nodo diferente de 0 es fuertemente conectada

Vídeo Complementario
Ejercicio
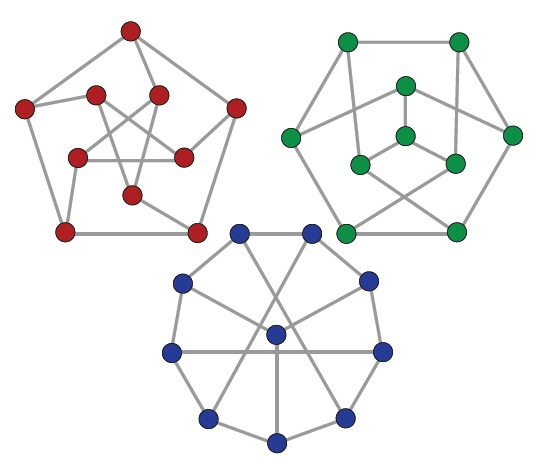
Dado un grafo con matriz de adyacencia
A) El grafo es euleriano
B) El grafo es conexo
C) Es un multigrafo








No hay comentarios.:
Publicar un comentario